
เมื่อต้นเดือนที่ผ่านมาผมได้ร่วมแข่ง TechJam ที่ KBTG จัด และพบว่าทีม "Meow Meow :3" ผู้ชนะการแข่งขันเลือกใช้ภาษา MiniZinc ในการแก้โจทย์ปัญหา และแก้ปัญหาได้อย่างรวดเร็วเป็นทีมแรกๆ เสียด้วย
ด้วยความอยากรู้อยากเห็นเลยกลับมาศึกษาภาษานี้บ้าง และพบว่ามันเป็นภาษาที่ไม่เหมือนภาษาอื่นๆ ที่คุ้นเคยเลย การเขียนโปรแกรมจะไม่ใช่การบอกลำดับการทำงานต่างๆ ให้คอมพิวเตอร์ไปทำตามแล้ว แต่จะเปลี่ยนไปมองว่าผลลัพธ์ที่ต้องการนั้นมีข้อจำกัดอะไรบ้าง หลังจากเขียนข้อจำกัดต่างๆ จนครบก็ปล่อยให้คอมพิวเตอร์ไปคิดวิธีหาคำตอบเอาเอง
เมื่อได้ฟังหลักการทำงานแล้ว โปรแกรมเมอร์หลายๆ คนอาจรู้สึกอึดอัดขัดใจอยู่บ้าง อย่างน้อยๆ ก็ตรงที่เราจะไม่รู้ลำดับขั้นตอนการทำงานเบื้องหลังว่าโปรแกรมกำลังทำอะไรอยู่ แต่สำหรับคนที่มาจากสายอื่น ผมคิดว่า MiniZinc น่าจะช่วยตัดทอนรายละเอียดอันซับซ้อนของการเขียนโปรแกรมลงไปได้ไม่น้อยเลยทีเดียว
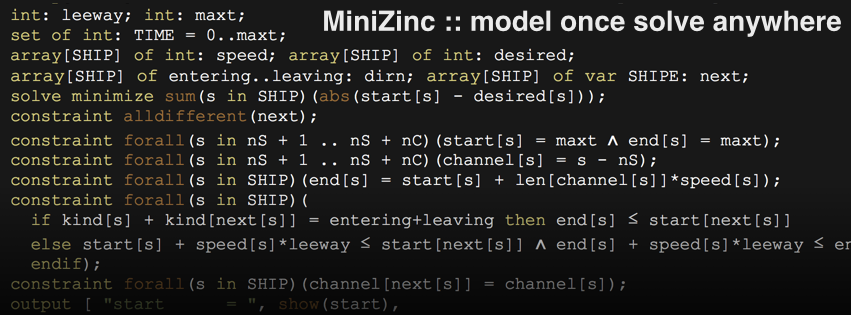
ความเป็นมาของ MiniZinc
ถ้าย้อนความกลับไปยังสมัยนักศึกษา เราอาจพอจำได้ลางๆ ว่าภาษาคอมพิวเตอร์นั้นมีด้วยกันหลายยุค ยุคแรกๆ ก็เป็นภาษาชั้นล่างที่ติดต่อกับฮาร์ดแวร์โดยตรง แล้วก็มีการพัฒนาต่อมาเรื่อยๆ จนปัจจุบันเรา (ส่วนใหญ่น่าจะ) ใช้ภาษาในยุคที่ 3-4 กันอยู่ เช่น C++, Python, JavaScript, R ซึ่งเป็นภาษาที่เราต้องป้อนคำสั่งเป็นลำดับขั้นตอนให้คอมพิวเตอร์ไปทำงานตามนั่นเอง
ส่วนภาษาคอมพิวเตอร์ในยุคที่ 5 นั้นจะซ่อนรายละเอียดปลีกย่อยที่โปรแกรมเมอร์ต้องคอยกำกับคอมพิวเตอร์ทุกขั้นตอน เปลี่ยนไปเป็นบอกว่าเราต้องการผลลัพธ์แบบไหน มีข้อจำกัดอะไรบ้างแทน โดยใช้การดำเนินการทางตรรกะมาอธิบายความสัมพันธ์และข้อจำกัดของผลลัพธ์ ภาษาในยุคนี้ที่หลายคนน่าจะเคยได้ยินชื่อก็เช่น Prolog
ด้าน MiniZinc นั้นก็เป็นภาษาโปรแกรมเชิงข้อจำกัดในยุคที่ 5 ที่ตั้งเป้าหมายว่าจะลดความยุ่งยากของภาษา Zinc และสร้างมาตรฐานการเขียนโปรแกรมเชิงข้อจำกัด ซึ่งมันออกเวอร์ชัน 1.0 ในปี 2009 จนถึงปัจจุบันได้เดินทางมาถึงเวอร์ชัน 2.2 แล้ว
โปรแกรมแรก!
ก่อนที่จะเจาะลึกลงไปดูรายละเอียดของคำสั่งต่างๆ เพื่อให้เขียนโปรแกรม MiniZinc แก้ปัญหาใดๆ ก็ได้ตามที่ใจต้องการ ผมคิดว่าเราควรเริ่มจากการเขียนโปรแกรมแรกอย่างรวดเร็วกันเลยดีกว่า และมันก็ไม่ควรจะเป็นเพียงแค่การพิมพ์ Hello world! เท่านั้นด้วย เพราะเราจะมาหาคำตอบของชีวิต, เอกภพ, และทุกสิ่งทุกอย่างกัน!
โดยเราจะเริ่มจากเปิด IDE ของ MiniZinc ขึ้นมา พิมพ์โค้ดตามที่จะเห็นข้างล่างนี้ลงไป แล้วเซฟโปรแกรมในชื่อ answer.mzn (สำหรับใครที่ขี้เกียจพิมพ์ตาม สามารถหาโค้ดทั้งหมดในบทความได้จาก Gist นี้)

โปรแกรมเราเพิ่งเขียนเสร็จนี้มี 4 ส่วนด้วยกัน ซึ่งก็คือ
- บรรทัดแรก บอกว่าคำตอบที่ต้องการหาเป็นตัวแปรประเภทใด ซึ่งในที่นี้ก็คือจำนวนเต็ม (
int) - สี่บรรทัดถัดมาบอกข้อจำกัดต่างๆ ของคำตอบที่เราต้องการหา อันได้แก่มันจะต้องอยู่ในช่วง 1 ถึง 100 และต้องหาร 2, 3, 7 ลงตัว
- คำสั่ง
solve satisfyเป็นคำสั่งสำหรับให้โปรแกรมเริ่มทำงานค้นหาคำตอบที่ตรงตามข้อจำกัด - บรรทัดสุดท้ายเป็นการพิมพ์ผลลัพธ์ ซึ่งถ้าเราทดลองใน MiniZinc IDE ก็อาจละคำสั่งนี้ได้
เมื่อรันโปรแกรมดังกล่าวด้วยการกด Ctrl-R ก็จะได้ผลลัพธ์กลับมาทางหน้าจอว่า 42 เป็นอันจบโปรแกรม
ขอให้จำโปรแกรมแรกของเรานี้ไว้ เพราะในหัวข้อถัดๆ ไปเราจะถอด-ประกอบ-เรียนรู้-ปรับปรุงจากมัน
รายละเอียดคำสั่ง MiniZinc
จากตัวอย่างโปรแกรมแรกของเรา แม้วากยสัมพันธ์ของ MiniZinc จะมีความแตกต่างจากภาษาที่เราคุ้นเคยในปัจจุบันพอสมควร แต่โดยหากค่อยๆ ดูไปทีละส่วนจะพบว่าไม่หนีกับภาษาอื่นเท่าใดนัก เพียงแค่เราเปลี่ยนวิธีมองหาผลลัพธ์ให้เขียนอยู่ในรูปของข้อจำกัดให้ได้ เท่านี้ก็น่าจะเบิกทางไปสู่การเขียนโปรแกรม MiniZinc ได้ไม่ยาก
รู้จักกับตัวแปร
อย่างที่ได้เห็นในโปรแกรมแรกของเราไปแล้วว่า เราสามารถประกาศตัวแปรขึ้นมาได้เลยโดยไม่ต้องกำหนดค่าตั้งต้น เพียงแค่ไปบอกว่าเราต้องการให้ตัวแปรดังกล่าวเป็นชนิดใดเท่านั้น ในการทำงานเบื้องหลังตัวแปรเหล่านี้จะถูกเปลี่ยนค่าไปเรื่อยๆ จนกว่าจะเจอค่าที่ตรงกับข้อจำกัด ซึ่งภาษา MiniZinc เรียกตัวแปรเหล่านี้ว่า "ตัวแปรตัดสินใจ" (decision variable)
แต่ยังมีตัวแปรอีกประเภทหนึ่งซึ่งไม่สามารถหรือไม่ควรเปลี่ยนค่า โดยเราอาจจะกำหนดมันขึ้นมาเพื่อย่นระยะเวลาที่ต้องพิมพ์เพราะใช้ค่านั้นบ่อยๆ ใน MiniZinc จะเรียกค่าเหล่านี้ว่า "พารามิเตอร์" (parameter) และประกาศมันได้ด้วยการตัดคำว่า var ออกไป พร้อมทั้งกำหนดค่าให้มันผ่านเครื่องหมาย = ในทันที ดังเช่นตัวอย่างต่อไปนี้

หรือเราอาจจะละการกำหนดค่าตั้งต้นให้พารามิเตอร์ลงไปในโค้ดโปรแกรมของเราก็ได้ ซึ่งจะทำให้ MiniZinc ถามเราซ้ำอีกทีตอนรันโปรแกรม ว่าเราต้องการให้พารามิเตอร์ที่ปล่อยว่างทิ้งไว้มีค่าเป็นเท่าไหร่ในการคำนวณครั้งนั้นๆ?
สำหรับชนิดของตัวแปรที่ MiniZinc รองรับ คือ
- จำนวนเต็ม
intมีค่าอยู่ระหว่าง ±(231-2) - จำนวนจริง
floatมีค่าอยู่ระหว่าง ±(1015-1) โดยค่าที่เล็กที่สุดที่ทำให้สองค่าแตกต่างกันอยู่ที่ประมาณ 5×10-324 - บูลีน
boolมีค่าเป็นtrueหรือfalse - สายอักขระ
stringสำหรับข้อความตัวอักษร -- ปัจจุบันตัวภาษายังไม่รองรับความสามารถในการแก้ปัญหาเพื่อหาข้อความตามข้อจำกัด
และจากชนิดตัวแปรข้างต้น เราสามารถนำมาสร้างเป็นตัวแปรชุดได้อีก 2 แบบ ดังนี้
- เซต
setสำหรับเก็บช่วงของค่าที่สนใจ โดยไม่สนใจตำแหน่งหรือค่าซ้ำ - อาเรย์
arrayสำหรับบอกค่าที่สนใจซึ่งผูกผันกับตำแหน่งต่างๆ ในตัวแปรชุด
ต่อไปนี้เป็นตัวอย่างการประกาศตัวแปรชุดทั้งแบบเซตและอาเรย์
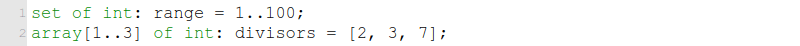
สังเกตว่าตัวแปรเซต range = 1..100 นั้น เป็นเซตของตัวเลขที่เป็นไปได้ทั้งหมดเมื่อถูกตรวจสอบด้วยข้อจำกัดแรก 1 <= answer /\ answer <= 100 ด้วยเช่นกัน MiniZinc ยอมให้เราประกาศตัวแปรโดยใช้เซตเป็นขอบเขตได้ทันที
ดังนั้น เราจึงสามารถแก้ไขโปรแกรมแรกของเราได้เป็น

เขียนข้อจำกัด
ข้อจำกัดใน MiniZinc นั้น ถ้ามองง่ายๆ ก็คงไม่ต่างจากการเขียน if-else หรือ filter ในภาษาที่เราคุ้นเคยเท่าใดนัก เพียงแค่เปลี่ยนตัวดำเนินการให้มีหน้าตาแบบคณิตศาสตร์มากขึ้น เช่น แทนที่จะเขียน && หรือ and ก็เปลี่ยนไปเขียนด้วย /\ แทน
เราสามารถรวบสามข้อจำกัดการหารลงตัวในโปรแกรมตัวอย่างให้เหลือเพียงข้อจำกัดเดียวที่เชื่อมกันด้วย /\ ได้เช่นนี้
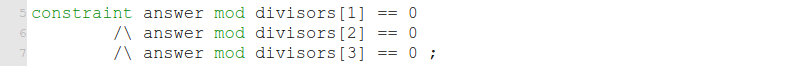
ซึ่งเราคงเห็นตั้งแต่ต้นแล้วว่า ทั้งสามพจน์ในข้อจำกัดนี้มีหน้าที่ตาเหมือนกันแทบจะทั้งหมด ส่วนที่ต่างก็เป็นเพียงตัวหารเท่านั้น ทำให้เราสามารถใช้ตัวบ่งปริมาณทั้งหมด forall มาช่วยกำจัดพจน์ซ้ำๆ เหล่านั้นได้ ซึ่งจะทำให้เขียนสั้นลงเหลือเพียง
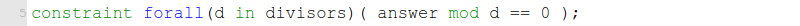
อนึ่ง สำหรับการเชื่อมกันของตัวดำเนินการแบบหรือ (\/) จะใช้ตัวบ่งปริมาณบางตัว exists แทนนั่นเอง
หาคำตอบที่ต้องการ
การสั่ง solve satisfy ตามโปรแกรมตัวอย่าง จะคืนคำตอบแรกที่โปรแกรมหาพบและจบการทำงานในทันที
แต่ในการแก้กำหนดการเชิงเส้น ค่าที่เราสนใจอาจไม่ใช่ค่าใดๆ ที่พบก็ได้ แต่เป็นค่าที่สูงสุด/ต่ำสุด จากค่าทั้งหมดที่ตรงตามข้อจำกัด ซึ่งเราสามารถบอกให้ MiniZinc หาค่าที่ตรงตามเงื่อนไขดังกล่าวได้เช่นกัน
โค้ดต่อไปนี้แก้การหาคำตอบที่สนใจในโปรแกรมตัวอย่าง ซึ่งจะให้ผลลัพธ์ที่แตกต่างออกไปจากการทดลองครั้งก่อนๆ ที่ผ่านมา

พิมพ์ผลลัพธ์จัดให้สวย
สำหรับโจทย์บางข้อ การไม่ใช้คำสั่ง output เพื่อจัดผลลัพธ์เอง ก็จะพิมพ์คำตอบออกมาได้อ่านง่ายพอสมควรอยู่แล้ว แต่หากต้องการจัดรูปแบบผลลัพธ์ ก็สามารถทำได้โดยส่งอาเรย์ของข้อความตัวอักษรเข้าไป โดยแทนที่ตัวแปรที่ต้องการแสดงด้วย \(var-name) เช่นนี้
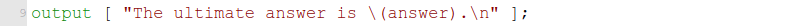
เวิร์คช็อปเพิ่มความเข้าใจ
เราได้เห็นตัวอย่างง่ายๆ ของการเขียนโปรแกรมใน MiniZinc ไปแล้ว ต่อไปนี้จะขอแนะนำโปรแกรมสำหรับแก้โจทย์ปัญหาที่น่าสนใจ พร้อมเทคนิคการเขียนโปรแกรมเพิ่มเติม
อักษรซ่อนเลข
เกมอักษรซ่อนเลข (cryptarithmetic) เป็นเกมที่ให้สมการ (ของเลขฐานสิบ) มาชุดหนึ่ง ซึ่งตัวเลขหลักต่างๆ ในสมการนั้นจะถูกแทนที่ด้วยตัวอักษร คำถามคือให้หาว่าตัวอักษรแต่ละตัวมีค่าเป็นเท่าใดบ้าง โดยตัวอักษรที่ไม่เหมือนกันจะต้องมีค่าไม่ซ้ำกันด้วย
ตัวอย่างเช่นสมการ SEND + MORE = MONEY นั้นมีค่าเท่ากับ 9567 + 1085 = 10652 นั่นเอง
ซึ่งเราสามารถเขียนเป็นโปรแกรมให้ MiniZinc ไปแก้ปริศนาได้ดังนี้

ส่วนที่น่าสนใจในโปรแกรมนี้ คือบรรทัดที่ 10-11 ที่เช็คว่าตัวอักษรแต่ละตัวต้องมีค่าไม่ซ้ำกัน
จะเห็นว่าเราสร้างตัวแปรเพิ่มขึ้นมาเพื่อใช้คำนวณข้อจำกัดนี้เพียงข้อเดียว หากเทียบกับการเขียนโปรแกรมโดยทั่วไปแล้ว ก็คงคล้ายกับการประกาศตัวแปรที่ระดับ global นั่นเอง
นี่ไม่ใช่การเขียนโปรแกรมที่ดีเท่าใดนัก และเราสามารถปรับปรุงมันได้โดยการสร้างเพรดิเคต (predicate) ซึ่งเปรียบได้กับการเขียนฟังก์ชันที่รับตัวแปรต่างๆ แล้วตอบกลับเป็นบูลีนว่าถูกหรือผิดตามข้อจำกัดที่สนใจ
เราสามารถเปลี่ยนโค้ดข้างต้นให้อยู่ในรูปของเพรดิเคตได้ ดังนี้

อนึ่ง สังเกตว่าเราใช้ตรรกะ "เมื่อและก็ต่อเมื่อ" (iff) เพื่อรับรองว่าสองข้างของตัวเชื่อมจะต้องเป็นจริงพร้อมกันหรือเท็จพร้อมกันเท่านั้น นี่เทียบได้กับเกต XNOR นั่นเอง
ซูโดกุ
เชื่อว่าคงไม่มีใครไม่รู้จักเกมซูโดกุ จากความรู้ MiniZinc ที่ผ่านๆ มา เราอาจเขียนโปรแกรมแก้โจทย์ซูโดกุที่เราสนใจข้อหนึ่งออกมาเป็นไฟล์ sudoku-solver.mzn ได้ดังนี้

แม้เราจะสามารถเขียนข้อจำกัดของปัญหาได้สั้นกระชับเข้าใจง่าย แต่ส่วนที่ยุ่งเหยิงที่สุดในโปรแกรมกลับกลายเป็นการป้อนข้อมูลแทน สำหรับโจทย์ข้อนี้นอกจากข้อมูลนำเข้าจะยืดยาวแล้ว การค่อยๆ ป้อนตัวเลขตำแหน่งต่างๆ ในตารางทีละตัวยังเสี่ยงต่อการพิมพ์ผิดอีกด้วย
เราอาจแก้โปรแกรมข้างต้น โดยเปลี่ยนบรรทัดที่เป็น constraint t[r,c] = x; ทั้งหมด ไปเป็นพารามิเตอร์ตารางตั้งต้น (ใส่เลข 0 แทนช่องที่ต้องการแก้โจทย์หาตัวเลข) พร้อมเพิ่มกฎการห้ามเปลี่ยนตัวเลขในตารางตั้งต้นที่ไม่ใช่เลข 0 เช่นนี้

ถึงนี่จะดูง่ายขึ้นมากแล้ว แต่มันก็ยังมีข้อเสียตรงที่ข้อมูลต่างๆ นั้นผูกติดแนบแน่นไปกับไฟล์โปรแกรมของเราอยู่ดี หากเราต้องการแก้โจทย์ซูโดกุเกมอื่น ก็ต้องทำสำเนาไฟล์นี้แล้วค่อยๆ เปลี่ยนค่าตัวเลขในตัวแปร s เอา ทั้งที่ส่วนตรรกะโปรแกรมไม่ได้เปลี่ยนเลยแม้แต่นิดเดียว
ทางออกสำหรับปัญหานี้ คือแยกพารามิเตอร์เฉพาะตัวของโจทย์ข้อนั้นๆ ไปไว้ในไฟล์ .dzn ที่ MiniZinc จัดเตรียมไว้ให้ ซึ่งก็คือ เราจะสร้างไฟล์ sudoku-input-1.dzn ขึ้นมา โดยมีเนื้อหาดังนี้

ส่วนที่ไฟล์โปรแกรม sudoku-solver.mzn ก็จะลบค่าพารามิเตอร์ตั้งต้นของ s ทิ้งไป เหลือไว้แค่การประกาศชนิดตัวแปรของ s เท่านั้นพอ
ทั้งนี้ทั้งนั้น ก่อนจะเริ่มรันโปรแกรมดังกล่าว (หรือโปรแกรมอื่นใดที่รับข้อมูลนำเข้าเป็นไฟล์) ก็อย่าลืมไปแก้ Configuration ใน IDE ให้ค่าของ Data file ชี้ไปยัง sudoku-input-1.dzn ด้วยนะ
จัดกระเป๋าเดินทาง
ปัญหาการจัดกระเป๋าเดินทาง (knapsack problem) กล่าวว่า ให้กระเป๋าเดินทางที่บรรจุน้ำหนักได้จำกัดที่ค่าหนึ่ง และของอีกหลายๆ ชิ้นซึ่งแต่ละชิ้นมีน้ำหนักและมูลค่าแตกต่างกันไป ถามว่าต้องเลือกหยิบของชิ้นใดใส่กระเป๋าบ้าง เพื่อให้ได้มูลค่ารวมของสิ่งของสูงสุด โดยน้ำหนักของสิ่งของที่เลือกต้องไม่เกินน้ำหนักที่กระเป๋าจะรับได้
ปัญหาดังกล่าวสามารถแปลงเป็นข้อจำกัดใน MiniZinc ได้ดังนี้

ข้อมูลตัวอย่างสำหรับปัญหาการจัดกระเป๋าเดินทาง ที่มีสิ่งของให้ตัดสินใจ 42 ชิ้น

จากเวลาคำนวณ 12 นาที ผมเข้าใจว่า MiniZinc น่าจะทดลองหยิบของด้วยทุกวิธีที่เป็นไปได้ จนมั่นใจในคำตอบสุดท้ายว่าการหยิบของที่ดีที่สุดคือ
knapsack = {1,8,9,10,12,15,16,20,21,22,24,25,27,29,32,33,34,38};
กำหนดการจำนวนเต็ม
สมมติว่าเราเปิดร้านอาหารแห่งหนึ่ง ซึ่งประกอบไปด้วย 2 เมนูด้วยกัน คือ
- แซลมอนซาซิมิ ราคา 129 บาท วัตถุดิบคือปลาแซลมอน 120 กรัม
- แซลมอนซูชิ ราคา 19 บาท วัตถุดิบคือปลาแซลมอน 15 กรัม และข้าว 10 กรัม
เราต้องการหา ว่าการขายอาหารแต่ละเมนูเป็นจำนวนเท่าใด ถึงจะให้รายได้สูงที่สุด?
หากตอนเริ่มต้นของวันเรามีวัตถุดิบคือแซลมอน 5 กิโลกรัม และข้าว 2 กิโลกรัม เมื่อนำเงื่อนไขต่างๆ มาเขียนมาเขียนเป็นระบบอสมการ จะได้
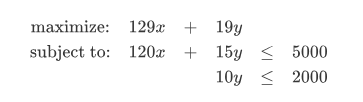
เมื่อพล็อตระบบอสมการออกมาดู ก็จะเห็นหน้าตาของบริเวณที่เป็นไปได้ (feasible region) ซึ่งก็คือบริเวณที่อยู่ด้านใต้ของเส้นทุกเส้น (ยกเว้นเส้นแกน) เช่นนี้
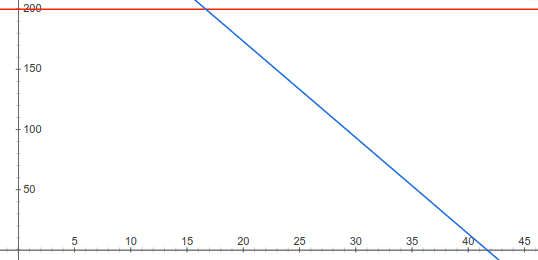
เส้นสีน้ำเงินแทนอสมการแรก และเส้นสีแดงแทนอสมการที่สอง
แน่นอนว่าเราคงไม่ขายอาหารแค่ครั้งละครึ่งจาน เราจึงต้องหาคำตอบด้วยกำหนดการจำนวนเต็ม (integer programming) ซึ่งสามารถเขียนเป็นโปรแกรมได้ดังนี้

ซึ่งจะให้คำตอบว่า เราควรขายซาซิมิ 17 ชุด และซูชิ 197 คำ ซึ่งจะทำให้มีรายรับสูงที่สุดที่ 5,936 บาท
สรุป
จากตัวอย่างต่างๆ ที่ได้เห็นกันไปนั้น แม้ MiniZinc จะไม่ได้เลือกอัลกอริทึมที่รวดเร็วที่สุดมาแก้ปัญหาก็ตาม แต่ด้วยไวยกรณ์และวากยสัมพันธ์ของมัน ก็ทำให้การเขียนโปรแกรมเพื่อตรวจสอบโมเดลทางคณิตศาสตร์ต่างๆ เป็นไปได้อย่างเรียบง่าย รวดเร็ว และลดข้อผิดพลาดต่างๆ ที่พบเจอได้ง่ายในภาษายุคเก่า
นอกจากนี้ การที่ตัวภาษาซ่อนรายละเอียดทางเทคนิคโปรแกรมมิ่งไปเกือบหมด และเลือกแต่ส่วนที่เป็นตรรกะคณิตศาสตร์พื้นฐานมาให้ใช้ ก็น่าจะทำให้ผู้ที่ไม่ได้มีพื้นด้านการเขียนโปรแกรมมาก่อน สามารถสร้างโมเดลทางคณิตศาสตร์ได้ง่ายขึ้นด้วย ซึ่งผมคิดว่านี่คือประโยชน์ที่แท้จริง เพราะเราสามารถนำมันไปใช้แก้ปัญหาต่างๆ ในโลกจริงได้อย่างมากมาย
สำหรับนักพัฒนาที่เชี่ยวชาญอัลกอริทึมแล้ว แม้ว่า MiniZinc จะไม่ได้ช่วยให้เขียนโปรแกรมที่ทำงานได้เร็วขึ้นก็ตาม แต่ผมคิดว่าการเขียนโปรแกรมในยุคที่ 5 ที่เป็นเชิงตรรกะและข้อจำกัด ก็เป็นแนวคิดที่มีคุณค่าให้ศึกษาไม่น้อยเลยทีเดียว ยิ่งเมื่อดูคู่ไปกับเทรนด์ปัญญาประดิษฐ์แล้ว นี่น่าจะเป็นอนาคตของการเขียนโปรแกรมในยุคหน้าอย่างแน่นอน








Comments
น่าสนใจมาก ขอบคุณครับ
+1 ขอบคุณด้วย
ขอบคุณครับ น่าสนใจมาก
แจ่มแมวเลยครับ
ต้องลองศึกษาดูบ้างละ
น่าสนใจจนต้องโหลดมาลองเลยครับ
ขอบคุณสำหรับข้อมูลที่แบ่งปันครับ
วากยสัมพันธ์ ...
สะดุดกับคำนี้เหมือนกัน .... ไม่ได้เห็นนานมาก ดูจากรูปประโยชน์มันน่าจะคือ syntax ป่ะฮะ
นับถือในความพยายามอธิบาย เข้าใจง่ายมากครับ ขอบคุณครับ
เทคโนโลยีไม่ผิด คนใช้มันในทางที่ผิดนั่นแหละที่ผิด!?!
+1
ผมลืมขอบคุณ ขอบคุณ @neizod ด้วยครับที่ตั้งใจเขียนมาให้อ่าน
ได้ความรู้ดีครับ เหมือนย่อยข่าวไปในตัวด้วย
เห็นอนาคตเลย อีกหน่อยไม่ต้องมีโปรแกรมเมอร์แล้ว
นึกถึง Prolog แฮะ
blog.semicolon.in.th
น่าสนใจครับ จะลองไปศึกษาดู
ขอบคุณสำหรับบทความดี ๆ ครับ...